Solve The System With The Initial Value
Solved Solve The System Dx Dt X With The Initial Value Chegg Com
Solve the system with the initial value. The question is why devilish minus six Swedish plus 10 by its a question and to initial conditions are given. Solving this system gives c 1 2 c 2 1 c 3 3. Y exp x z exp x u 0.
Rewrite the van der Pol equation second-order where is a scalar parameter by making the substitution. However y 0 also satisfies the differential equation and y0 0. A x u x y b y u x y f.
X 1 x 2 x 1 3 6 x 2 1 2 x 1 5 2 x 2 x 2 3 1 x 1 x 2 x 1 3 6 x 2 1 2 x 1 5 2 x 2 x 2 3 1. I rod about cutting my system in real and imaginary part and solve separately but my ODE systems rhs involves products between dependent variables themselves and their complex conjugates. The function fu D p u is not Lipschitz continuous near u D 0 since f0u D 12 p u1as u.
1 point Solve the system 354 dt 9 22 with the initial value x0 xt. To return implicit solutions of the differential equation set the Implicit option to true. Solve the differential equation.
Used as an initial value for the system The additional initial values needed for the solving the system Guessed. U y z 0. U1t 2e3te39t 1 3 cost u2 t e3 t 239.
The initial value problem may fail to have a unique solution over any time interval if this initialvalue is imposed. F u x u x x 0. Solve the system dxdt x with x 0.
F 0 a f 0a f 0 a. B dxdt 2 -1 4 6 x with the initial value.
Solved Solve The System Dx Dt With The Initial Value X 0 Chegg Com
Solved Solve The System Dx Dt X With The Initial Value Chegg Com
Solved Solve The System Dx Dt With The Initial Value Chegg Com
Solved Solve The System Dx Dt X With The Initial Value Chegg Com
Solved Solve The System Dx Dt X With The Initial Value Chegg Com
1 Point Solve The System8 4dx Dt22with The Initia Itprospt
Solving System Of Ode With Initial Value Problem Ivp Mathematics Stack Exchange
Solved 1 Point Solve The System Dx Dt 1 1 6 6 X Chegg Com
Solved Points Consider The Initial Value Problem 1 8 4 U G0 4 A Find The Eigenvalue A An Eigenvector 01 And Generalized Eigenvector 0z For The Coefficient Matrix Of This Linear
Lfooaergzrk Zm
Solution Of System 3 1 With Initial Value X 0 100 200 2500 Download Scientific Diagram
A Solution Of System 1 4 With The Initial Value 0 0 0 6 0 3 Download Scientific Diagram
Solved Point Solve The System With The Initial Value C U Sexp 2 3exp 3
Solved Solve The System Dx Dt 16 6 36 14 X With The Chegg Com
Solving Initial Value Problems Using Laplace Transforms Krista King Math Online Math Tutor
Systems Of Equations Solver Wolfram Alpha
Math 2403 Practice Final 1 Solve The Initial Value Problem Dx Dt
How To Solve Initial Value Problems Youtube
Amazon Com On Initial Value Problems And Its Applications On Solving Initial Value Problems And Its Applications To Decrease Dangers Of Lead And Cold Pills 9783659113734 Awad Abd Alrazak Heba Naji Mohammed Tawfiq
Solution Z T µ Of System 12 With Initial Value Z 0 µ 0 6 For Download Scientific Diagram
Apply The Eigenvalue Method To Find A General Solution Of The Given System If Initial Values Are Gi Youtube
Solved A System Of Ordinary Differential Equations Has General Solution X T 24 26 Find The Parameters C1 And C2 If The Initial Value Is Z 0 Acie 2c1e 3c2e Sce
Solving Initial Value Problems Using Laplace Transforms Krista King Math Online Math Tutor
1
Answered Consider The Initial Value Problem Bartleby
Ch 1 2 Solutions Of Some Differential Equations Ppt Download
Solved Solve The System X 1 10x 1 8x 2 X 2 12x 1 Chegg Com
Gosuoqee6rthom
1 Point Solve The System 14 36 Dx Dt 6 16 With The Initial Value 20 X 0 Homeworklib
11 Initial Value Problems System
Solution Of System 3 1 With Initial Value X 0 100 200 2500 Download Scientific Diagram
11 Initial Value Problems System
Basic Initial Value Problem Mathematics Stack Exchange
Differential Equations Solved Examples Convert The Initial Value Problem Into A First Order System Give The Matrix A Which Determines The System And The Initial Vector X 0 Y 3y 10y
Solved 5 Points Solve The System T 5y D 1c 8y With Tfie Initial Value 0 6 3 0 C T Y T
Numerical Solution I µi I µi Of System 51 For Initial Value I Download Scientific Diagram
On Initial Value And Boundary Value Problem Of Linear Differential Algebra System
Answered Given The System Of Equations 1 5 Bartleby
Initial Value Problem Youtube
1 Point Consider The Initial Value Problem My 34 Cy 39 Ky F T Y 0 0 Y 39 0 0 Modeling The Motion Of Homeworklib
Solved 1 2 1 Consider The System Of Equations Given By Find A Fundamental Matrix For The System X T B Find The Matrix Exponential T Eat Ofthe System E T Solve The Initial
Solved Solve The System Dxdt 2 1 51 5 1 Xdxdt 21 5 1 5 1 X Chegg Com
Time Series Solution Of The System 1 4 With Initial Values 180 6 Download Scientific Diagram
How To Solve Linear Differential Equations Initial Value Problems Krista King Math Online Math Tutor
Suppose You Wanted To Check Whether The Initial Value Itprospt
Suppose We Are Given A Differential Equation And Initial Condition Then We Can Approximate The Solution To The Differential Equation By Its Linearization Ppt Download
Solve A System Of First Order Odes Using Explicit Euler Method Youtube
2
1
Find the particular solution for the system of differential equations given below with the initial values x10 33 and x20 16.
We will now discuss the Runge-Kutta method for solving such. Therefore one way to solve the problem is to reverse the Riccati equation in order to turn the final-value problem into an initial-value problem and find a numerical solution between time 0 and t_f using a standard ODE integrator. Solving this system gives c 1 2 c 2 1 c 3 3. Give your solution in real form. Rewrite the problem as a system of first-order ODEs. Sol dsolve eqn sol. Y eAty_0 in your case we have. So first real light oxidant equation. The solution at the end of the interval is compared with the specified boundary conditions.
Dsolve returns an explicit solution in terms of a Lambert W function that has a constant value. Euler method is simplistic approach for such problems but it comes with large inaccuracy. Heat transfer problem using fourth-order Runge Kutta. A x u x y b y u x y f. U0 1 9u 24u2 5cost 1 3 sint u0 2 24151 9cos t 1 3 sin with initial values u10 43 and u20 23. Rewrite the problem as a system of first-order ODEs. Click here if solved 34.
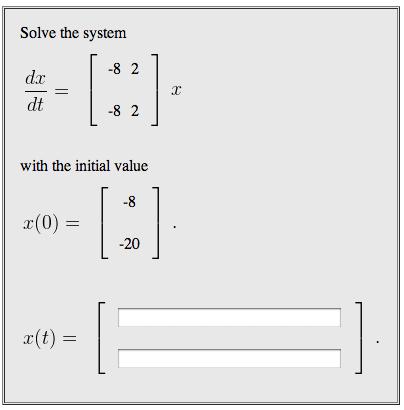
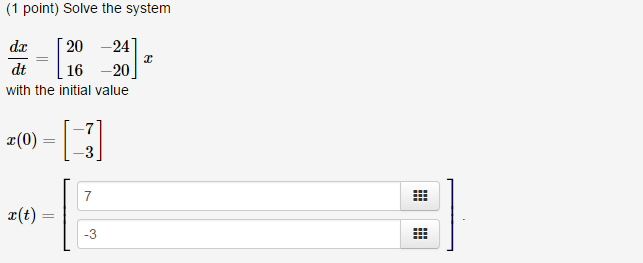
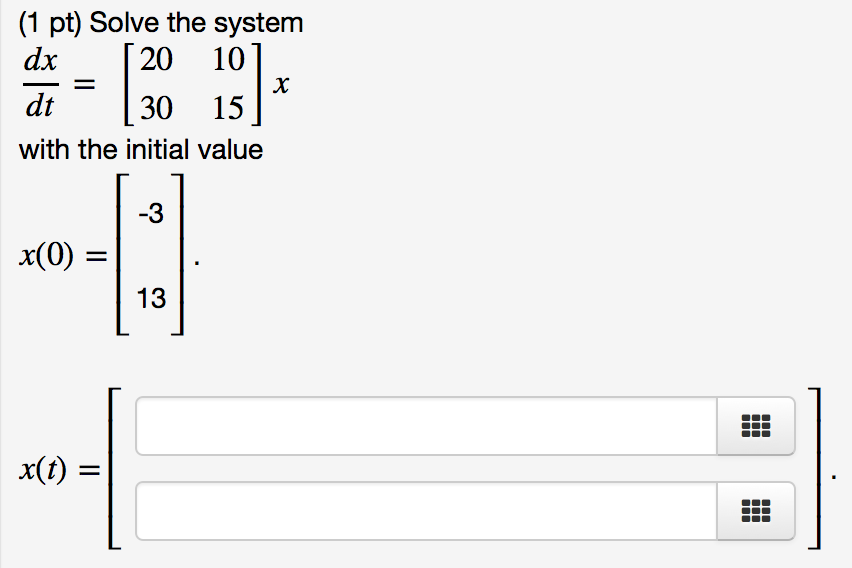
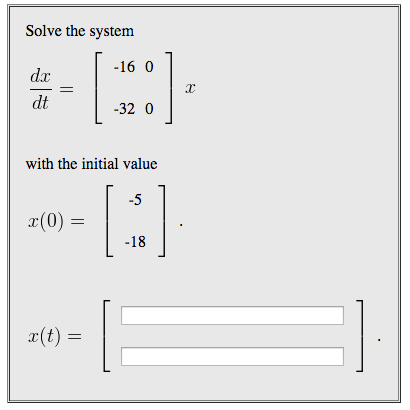
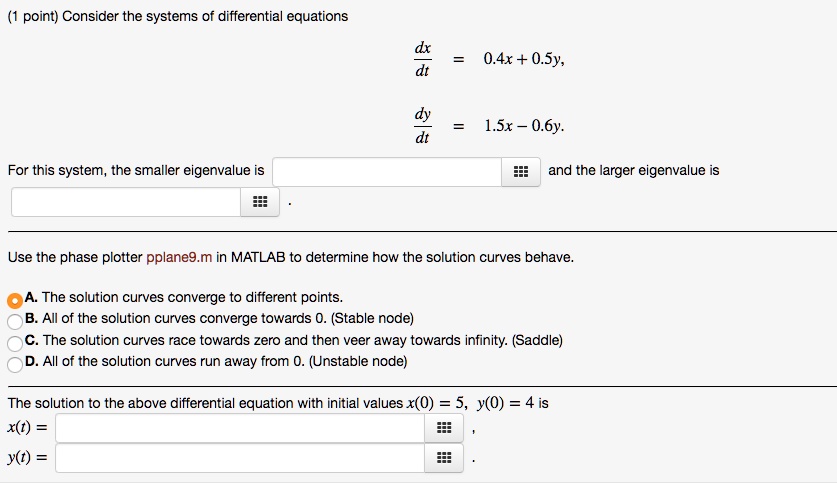
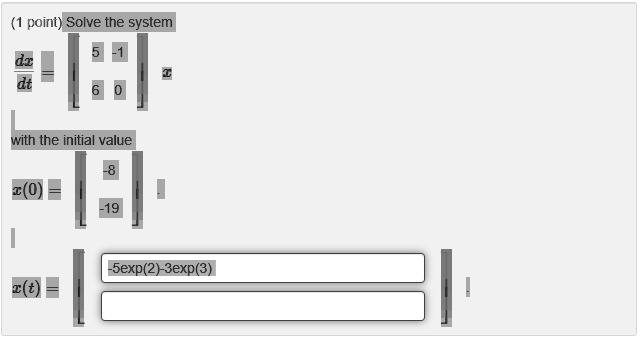
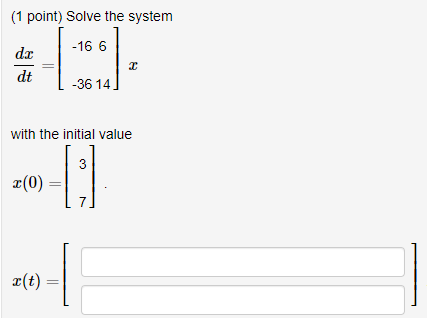
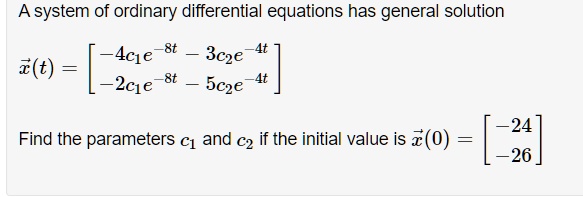
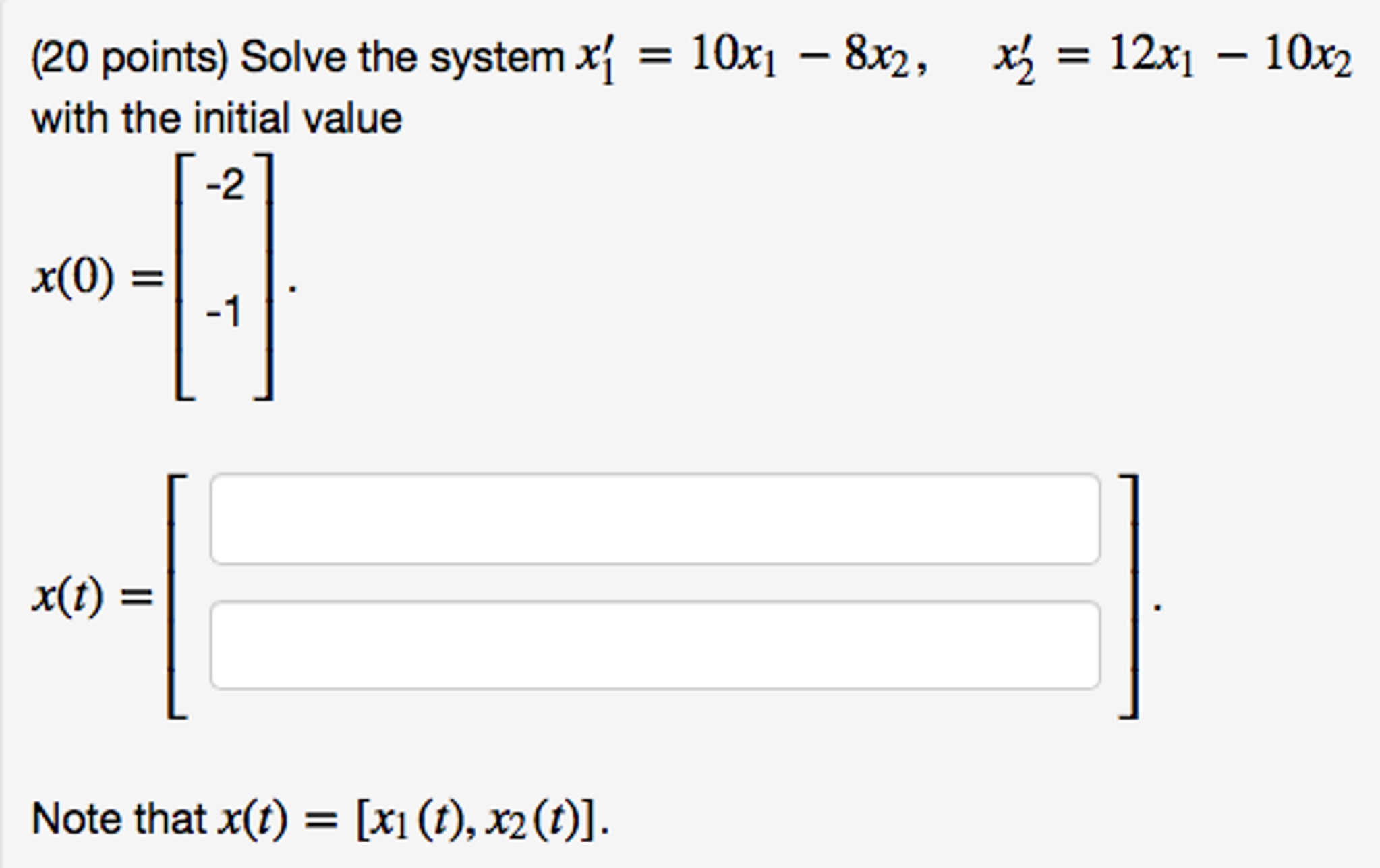
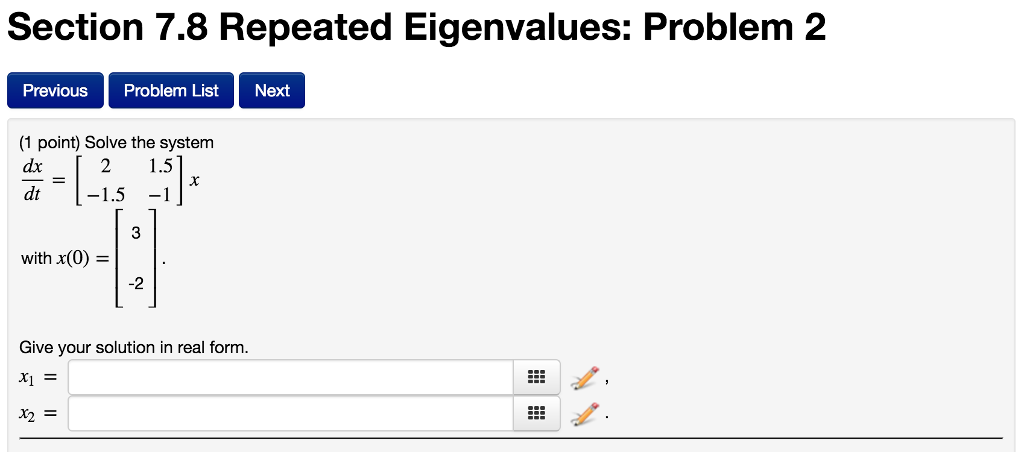
Post a Comment for "Solve The System With The Initial Value"